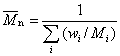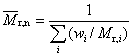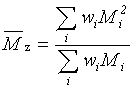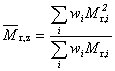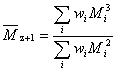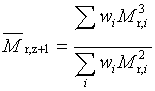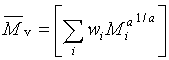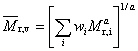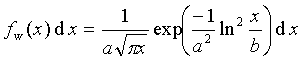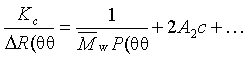|
Termín
|
|
Definice
|
|
1.1 |
relativní molekulová hmotnost |
doporučený symbol: Mr |
| |
|
Poměr průměrné hmotnosti molekuly odpovídající vzorci látky k jedné dvanáctině hmotnosti atomu nuklidu 12C.
Poznámka
Viz definice 1.2. |
|
1.2 |
molární hmotnost |
doporučený symbol: M
Hmotnost dělená látkovým množstvím. Poznámky
1. Molární hmotnost se obvykle vyjadřuje v jednotkách g/mol nebo kg/mol. Číselné hodnoty molární hmotnosti v jednotkách g/mol a relativní molekulové hmotnosti jsou stejné.
2. Relativní hmotnost je pouhým číslem a nesmí se k ní připojovat žádné jednotky.
3. Užívání daltonu jako jednotky hmotnosti, totožné s atomovou hmotnostní jednotkou, se nedoporučuje.
4. Termíny “molární” a “molekulový” je možno užít také pro částice složené z více než jedné molekuly, jako jsou komplexy, agregáty, micely atd.
5. V symbolu Mr, doporučeném pro relativní molekulovou hmotnost, se může index r vynechat, není-li to na úkor jednoznačnosti. |
|
1.3 |
polymerizační stupeň,
stupeň polymerizace |
doporučený symbol: X
doporučená zkratka: DP
Počet monomerních jednotek v molekule polymeru. |
|
1.4 |
termodynamicky ekvivalentní koule |
Koule, která je neprostupná pro jiné koule a vykazuje týž vyloučený objem (viz 3.1.9) jako skutečná molekula polymeru. |
|
1.5 |
intramolekulární interakce krátkého dosahu |
Sterická či jiná interakce mezi atomy, mezi skupinami nebo mezi atomy a skupinami ležícími v řetězci blízko sebe.
Poznámky
1. Interagující atomy nebo skupiny jsou v typickém případě odděleny méně než deseti po sobě následujícími vazbami řetězce.
2. Slovo “intramolekulární” je možno vynechat, není-li to na úkor jednoznačnosti. |
|
1.6 |
intramolekulární interakce dalekého dosahu |
Interakce mezi segmenty, které v řetězci leží daleko od sebe a které se v důsledku ohebnosti molekuly občas k sobě přibližují.
Poznámky
1. Tento typ interakce má úzký vztah k vyloučenému objemu segmentu (viz 3.1.8), který je projevem interakcí segmentů a molekul rozpoustědla.
2. Slovo “intramolekulární” je možno vynechat, není-li to na úkor jednoznačnosti. |
|
1.7 |
neporušené rozměry |
Rozměry skutečného nahodilého polymerního klubka (viz 1.15) ve stavu theta (viz 3.1.5). |
|
1.8 |
porušené rozměry |
Rozměry skutečné ho nahodilého polymerního klubka (viz 1.15), které není ve stavu theta (viz 3.1.5). |
|
1.9 |
gyrační poloměr |
doporučené symboly: 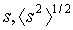
Parametr charakterizující velikost částice jakéhokoli tvaru. U tuhé částice, skládající se z hmotných elementů o hmotnosti mi umístěných ve vzdálenosti ri od těžiště částice, je gyrační poloměr s definován jako druhá odmocnina hmotnostního průměru veličiny ri2 všech hmotných elementů, tj.
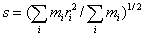
Není-li částice tuhá, uvažuje se průměr přes všechny konformace, tj.
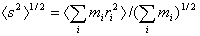
Poznámka
Pro označení neporušených rozměrů (viz 1.7) se užívá indexu nula, tedy 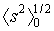 . . |
|
1.10 |
vektor spojnice konců |
doporuč ený symbol: r
Vektor spojující oba konce řetězce lineárního polymeru v dané konformaci. |
|
1.11 |
vzdálenost konců |
doporučený symbol: r
Délka vektoru spojnice konců (viz 1.10). |
|
1.12 |
odmocnina střední kvadratické vzdálenosti konců |
doporučený symbol: 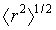
Druhá odmocnina střední kvadratické vzdálenosti konců (viz 1.11) řetězce lineárního polymeru průměrované přes všechny konformace řetězce. U volně skloubeného řetězce (viz 1.16) skládajícího se z N segmentů, z nichž každý má délku L, je 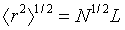 . .
Poznámky
l. Pro označení neporušených rozměrů (viz 1.7) se užívá indexu nula, tedy 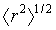 . .
2. Užívá-li se tento termín opakovaně a není-li to na úkor jednoznačnosti, může se použít zkráceného názvu “vzdálenost konců”. |
|
1.13 |
charakteristický poměr |
doporučený symbol: CN (C¥
, když N ®
¥
)
Poměr střední kvadratické vzdálenosti konců (viz 1.12) á
r2ñ
0 řetězce lineárního polymeru ve stavu theta (viz 3.1.5) k N.L2, kde N je počet tuhých úseků v hlavním řetězci a L je délka každého z nich; nemají-li všechny tuhé úseky touž délku, použije se střední kvadratické hodnoty veličiny L, tj.
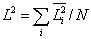
Poznámka
U jednoduchých jednopramenných řetězců se za tuhé úseky považují vazby. |
|
1.14 |
obrysová délka |
Maximální vzdálenost konců (viz 1.11) řetězce lineárního polymeru.
Poznámky
1. U jednopramenné molekuly polymeru se obrysovou délkou obvykle míní vzdálenost konců řetězce protaženého do konformace, při níž jsou všechny vazby v poloze trans. U řetězců se složitou strukturou může být obrysová délka zjistitelná jen přibližně.
2. Někdy se termínem “obrysová délka” označuje součet délek všech vazeb hlavního řetězce jednopramenné molekuly polymeru. Užívat termínu v tomto smyslu nedoporučujeme. |
|
1.15 |
nahodilé klubko,
statistické klubko |
Úplný soubor prostorových uspořádání řetězovité molekuly s velkým počtem segmentů, které v průběhu času nahodile mění vzájemnou orientaci, za podmínek, kdy řetězec není vystaven vnějším omezením, která by ovlivňovala jeho konfo rmaci.
Poznámka
Není-li roztok řetězovitých molekul ve stavu theta (viz 3.1.5), mění segmenty vzájemnou orientaci jen přibližně nahodile. |
|
1.16 |
volně skloubený řetězec |
Hypotetická lineární řetězovitá molekula skládající se z nekonečně tenkých, přímých a stejně dlouhých segmentů; každý segment může nabývat všech prostorových orientací se stejnou pravděpodobností, nezávisle na svých sousedech.
Poznámka
U modelů, jejichž segmenty nemají stejnou délku, se používá názvu řetězec typu “nahodilé procházky”. |
|
1.17 |
ekvivalentní řetězec |
Hypotetický volně skloubený řetězec (viz 1.16) s týmiž hodnotami střední kvadratické vzdálenosti konců (viz 1.11) a obrysové délky (viz 1.14), jaké má skutečný řetězec polymeru ve stavu theta (viz 3.1.5). |
|
1.18 |
statistický segment |
Segment skutečného řetězce polymeru, který se z hlediska uvažované vlastnosti chová prakticky stejně jako segment volně skloubeného řetězce (viz 1.16). |
|
1.19 |
volně otáčivý řetězec |
Hypotetická lineární řetězovitá molekula bez interakcí krátkého a dalekého dosahu (viz 1.5 a 1.6) skládající se z nekonečně tenkých, přímých segmentů stejné délky, spojených v určitém vazebném úhlu; torzní úhly vazeb mohou nabývat všech hodnot se stejnou pravděpodobností. |
|
1.20 |
sterický faktor |
doporučený symbol: s
Poměr odmocniny střední kvadratické vzdálenosti konců (viz 1.12) řetězce polymeru s neporušenými rozměry (viz 1.7), á
r2ñ
01/2, k odmocnině střední kvadratické vzdálenosti konců volně otáčivého řetězce (viz 1.19) s touž strukturou, á
r2ñ
0,f1/2, tj. (á
r2ñ
0/á
r2ñ
0,f)1/2 v limitě pro nekonečnou délku řetězce.
Poznámka
Sterický faktor odráží účinek zábran volné rotace. |
|
1.21 |
červovitý řetězec,
spojitě zakřivený řetězec |
Hypotetická lineární makromolekula skládající se z nekonečně tenkého spojitě zakřiveného řetězce; směr zakřivení je v kterémkoli bodu nahodilý.
Poznámky
1. Model popisuje celé spektrum řetězců s různým stupněm tuhosti, od tuhých tyčinek až k nahodilým klubkům (viz 1.15), a je obzvláště užitečný k popisu tuhých řetězců.
2. V literatuře se tento řetězec někdy označuje jako Porodův a Kratkyho řetězec. |
|
1.22 |
perzistenční délka |
doporučený symbol: a
Průměrná délka průmětu vektoru spojnice konců (viz 1.10) na tečnu vedenou k obrysu řetězce na jeho konci, v limitě pro nekonečnou délku řetězce.
Poznámka
Perzistenční délka je základní charakteristikou červovitého řetězce (viz 1.21). |
|
1.23 |
krátká větev |
Oligomerní výhonek z makromolekulárního řetězce. |
|
1.24 |
dlouhá větev |
Polymerní výhonek z makromolekulárního řetězce. |
|
1.25 |
index větvení |
doporučený symbol: g
Parametr charakterizující účinek dlouhých větví (viz 1.24) na velikost rozvětvené makromolekuly v roztoku a definovaný jako poměr středního čtverce gyračního poloměru (viz 1.9) rozvětvené molekuly, á
sb2ñ
, ku střednímu čtverci gyračního poloměru jinak identické lineární molekuly, á
sl2ñ
, o téže relativní molekulové hmotnosti (viz 1.1), v témže rozpoustědle a při téže teplotě, tj. g=á
sb2ñ
/á
sl2ñ
. |
|
1.26 |
sít' |
Vysoce rozvětvená polymerní struktura, kde každá konstituční jednotka je propojena se všemi ostatními konstitučními jednotkami a s makroskopickým fázovým rozhraním mnoha trvalými cestami vedoucími strukturou; počet cest vzrůstá s průměrným počtem vazeb mezi jednotkami; průměrné délky cest musí být souměřitelné s velikostí struktury.
Poznámka
V systémech vykazujících kaučukovou elasticitu a obvykle i u jiných systémů je počet různých cest velmi vysoký, avšak ve většině případů existují některé konstituční jednotky, které jsou spojeny jedinou cestou. Někdy se jako sít' označuje i struktura, která vícenásobné cesty neobsahuje. |
|
1.27 |
mikrogel |
Sít' mikroskopických rozměrů. |
|
1.28 |
kopolymerní micela |
Micela vytvořená jednou nebo více molekulami blokového či roubovaného kopolymeru v selektivním rozpouštědle (viz 3.1.14). |
|
Termín |
|
Definice |
|
2.1 |
heterogenita ve složení |
Rozdílnost elementámího složení jednotlivých molekul vyskytující se obvykle v kopolymerech. |
|
2.2 |
konstituční heterogenita |
Rozdínost konstituce jednotlivých molekul v polymerech, jejichž molekuly mají stejné elementární složení.
Poznámka
Příkladem je polymer složení z lineárních a rozvětvených molekul; jiným příkladem je statistický kopolymer obsahují dvě izomerní konstituční jednotky. |
|
2.3 |
uniformní polymer, monodisperzní polymer |
Polymer složený z molekul, které jsou z hlediska rela tivní molekulové hmotnosti (viz 1.1) i konstituce jednotné.
Poznámky
1. Polymer obsahující směs lineárních a rozvětvených řetězců (všechny s jednotnou relativní molekulovou hmotností) není uniformní.
2. Kopolymer obsahující lineární molekuly s jednotnou relativní molekulovou hmotností a s jednotným elementárním složením, avšak s rozdílným pořadím různých typů monomerních jednotek, není uniformní (např. kopolymer obsahující molekuly s nahodilým i blokovým uspořádáním monomerních jednotek).
3. Polymer, který je uniformní bud' pouze z hlediska relativní molekulové hmotnosti nebo pouze z hlediska konstituce, se může označit termínem “uniformní”, použije-li se vhodný přívlastek (např. “polymer uniformní z hlediska relativní molekulové hmotnosti”).
4. Přídavná jména “monodisperzní” nebo “polydisperzní” (viz 2.4) jsou v literatuře hluboce zakořeněna, přestože jsou nevýstižná a rozporná. Jsou však běžně používána a budou se patrně ještě nějakou dobu používat; je nicméně žádoucí nahradit je výstižnějšími termíny. Po rozsáhlém hledání možných náhrad byly vybrány nové termíny “uniformní” a “neuniformní” (viz 2.4), kterým by nyní měla být dávána přednost. |
|
2.4 |
neuniformní polymer, polydisperzní polymer |
Polymer obsahující molekuly neuniformní z hlediska relativní molekulové hmotnosti (viz 1.1) nebo z hlediska konstituce nebo z obou hledisek.
Poznámka
Viz 2.3, poznámka 3. |
|
2.5 |
průměr molární hmotnosti, průměr relativní molekulové hmotnosti (průměrná molární hmotnost, průměrná relativní molekulová hmotnost) |
doporučené symboly : 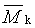 nebo nebo 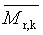
V obou symbolech určuje index k typ průměru.
Jakýkoli průměr molární hmotnosti (viz 1.2) nebo průměr relativní molekulové h motnosti (viz 1.1) neuniformního polymeru.
Poznámky
1. V zásadě je možné definovat nekonečný počet průměrů molární hmotnosti, avšak jen několik typů průměrů lze přímo experimentálně stanovit. Nejdůležitější průměry se definují jednoduchými momenty distribučních funkcí (viz 2.13) a získávají se metodami použitelnými pro systémy v termodynamické rovnováze, jako jsou osmometrie, rozptyl světla a sedimentační rovnováha. Hydrodynamické metody poskytují zpravidla složitější průměry molární hmotnosti.
2. Každý průměr molární hmotnosti může být definován pomocí hmotnostních zlomků nebo molárních zlomků. V tomto dokumentu je uvedeno pouze několik důležitých průměrů molární hmotnosti definovaných pomocí hmotnostních zlomků, wi, molekul s molární hmotností Mi. Tyto definice mají velmi úzký vztah k experimentálnímu stanovení průměrů molární hmotnosti. |
|
2.6 |
početně průměrná molární hmotnost |
doporučený symbol: 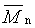
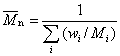
|
| |
početně průměrná relativní molekulová hmotnost |
doporučený symbol: 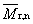
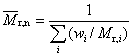
Symboly jsou vysvětleny pod heslem “průměr molární hmotnosti”, 2.5. |
|
2.7 |
hmotnostně průměrná molární hmotnost |
doporučený symbol: 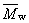
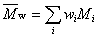
|
| |
hmotnostně průměrná relativní molekulová hmotnost |
doporučený symbol: 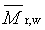
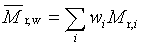
Symboly jsou vysvětleny pod heslem “průměr molární hmotnosti”, 2.5. |
|
2.8 |
z-průměrná molární hmotnost |
doporučený symbol: 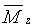
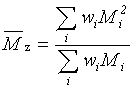
|
| |
z-průměrná relativní molekulová hmotnost |
doporučený symbol. 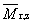
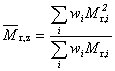
Symboly jsou vysvětleny pod heslem “průměr molární hmotnosti”, 2.5. |
|
2.9 |
(z+1)-průměrná molární hmotnost |
doporučený symbol: 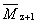
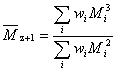
|
| |
(z+1)-průměrná relativní molekulová hmotnost |
doporučený symbol: 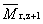
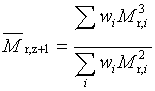
Symboly jsou vysvětleny pod heslem “průměr molární hmotnosti”, 2.5. |
|
2.10 |
viskozitně průměrná molární hmotnost |
doporučený symbol: 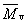
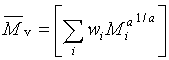
|
| |
viskozitně průměrná relativní molekulová hmotnost |
doporučený sy mbol: 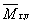
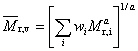
kde a je exponent v Markově-Houwinkově rovnici (viz 3.2.25), [h
]= K.Ma; ostatní symboly jsou vysvětleny pod heslem “průměr molární hmotnosti”, 2.5.
Poznámka
Exponent a není totožný s nastavitelným parametrem některých distribučních funkcí (viz 2.16 až 2.20) ani s perzistenční délkou (viz 1.22). |
|
2.11 |
zdánlivá molární hmotnost, zdánlivá relativní molekulová hmotnost |
doporučený symbol: Mapp
doporučený symbol: Mr,app
Molární hmotnost a relativní molekulová hmotnost vypočítaná z experimentálních dat bez použití příslušných korekcí, jako jsou korekce na konečnou koncentraci asociaci, preferenční solvataci, heterogenitu ve složení (viz 2.1), konstituční h eterogenitu (viz 2.2) apod. |
|
2.12 |
průměrný polymerizační stupeň |
doporučený symbol: 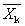 ,
kde k určuje typ průměru. Jakýkoli průměr polymerizačního stupně (viz 1.3) polymeru.
Poznámka
Definice 2.5 až 2.10 platí pro průměrný stupeň polymerizace, zamění-li se ve vzorcích M za X. |
|
2.13 |
distribuční funkce |
Normovaná funkce udávající relativní množství podílu polymerní látky s určitou hodnotou nebo rozsahem hodnot náhodné proměnné nebo proměnných.
Poznámky
l. Distribuční funkce mohou být diskrétní (nespojité), tj. definované pouze pro určité specifikované hodnoty náhodné proměnné (proměnných), nebo spojité, tj. definované pro libovolnou hodnotu náhodné proměnné (proměnných) ležící v daných mezích. V oboru polymerů je většina distribucí svou povahou diskrétní, je však často výhodné považovat je za spojité nebo používat distribuční funkce, které jsou svou povahou spojité.
2. Distribuční funkce mohou být integrální (neboli kumulativní), vyjadřující podíl populace, pro který je náhodná proměnná menší nebo rovna dané hodnotě. Alternativně to mohou být diferenciální distribuční funkce (neboli pravděpodobnostně hustotní funkce) vyjadřující podíl populace (i infinitezimální), pro který náhodná proměnná (náhodné proměnné) leží uvnitř intervalu (i infinitezimálního) svého oboru.
3. Má-li být funkce normována, je třeba, aby: (i) pro diskrétní diferenciální distribuční funkci byl součet hodnot funkce pro všechny možné hodnoty náhodné proměnné (náhodných proměnných) roven jedné; (ii) pro spojitou diferenciální distribuční funkci byl integrál přes celý rozsah náhodné proměnné (náhodných proměnných) roven jedné; (iii) pro integrální (kumulativní~ distribuční funkci byla hodnota funkce pro horní mez náhodné proměnné (náhodných proměnných) rovna jedné. |
|
2.14 |
početní distribuční funkce |
Distribuční funkce, pro kterou je množství podílu látky s určitou hodnotou nebo rozsahem hodnot náhodné proměnné (proměnných) vyjádřeno molárním zlomkem. |
|
2.15 |
hmotnostní distribuční funkce |
Distribuční funkce, pro kterou je množství podílu látky s určitou hodnotou nebo určitým rozsahem hodnot náhodné proměnné (proměnných) vyjádřeno hmotnostním zlomkem. |
|
2.16 |
Schulzova-Zimmova distribuce |
Spojitá distribuce s diferenciální hmotnostní distribuční funkcí (viz 2.15) ve tvaru
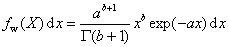
kde x je náhodná proměnná charakterizující délku řetězce, jako je relativní molekulová hmotnost (viz 1.1) nebo polymerizační stupeň (viz 1.3), a a b jsou kladné nastavitelné parametry a G
(b+1) je gamma funkce argumentu (b+1). |
|
2.17 |
nejpravděpodobnější distribuce |
Diskrétní distribuce s diferenciální hmotnostní distribuční funkcí (viz 2.15) ve tvaru
fw(x)=a2 x(1-a)x-1
Vysvětlení symbolů viz 2.16.
Poznámky
1. Pro velké hodnoty x konverguje nejpravděpodobnější distribuce ke zvláštnímu případu Schulzovy-Zimmovy distribuce (viz 2.16) s hodnotou b = 1.
2. V literatuře je tato distribuce někdy označována jako Floryho distribuce ne bo Schulzova-Floryho distribuce. |
|
2.18 |
Poissonova distribuce |
Diskrétní distribuce s diferenciální hmotnostní distribuční funkcí (viz 2.15) ve tvaru
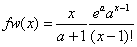
Vysvětlení symbolů viz 2.16. |
|
2.19 |
Tungova distribuce |
Spojitá distribuce s diferenciální hmotnostní distribuční funkcí (viz 2.15) ve tvaru
fw(x)dx=abxb-1 exp (axb) dx
Vysvětlení symbolů viz 2.16. |
|
2.20 |
logaritmická normální distribuce |
Spojitá distribuce s diferencíální hmotnostní distribuční funkcí (viz 2.15) ve tvaru
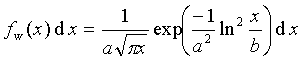
Vysvětlení symbolů viz 2.16. |
|
2.21 |
korekce na polymolekularitu |
Korekce, používaná ve vztazích mezi vlastností a molární hmotností b (viz 1.2) nebo relativní molekulovou hmotností (viz 1.1), získaná pro polymery neuniformní (viz 2.4) vzhledem k relativní molekulové hmotnosti tak, aby odpovídající vztah platil i pro polymery přísně uniformní (viz 2.3) vzhledem k relativní molekulové hmotnosti. |
|
Termín |
|
Definice |
|
3.1.1 |
zředěný roztok |
Roztok, v kterém je součet objemů domén zaujímaných molekulami nebo částicemi rozpuštěné látky podstatně menší než celkový objem roztoku
Poznámka
Termín “doména” označuje nejmenší konveční těleso, které pojme molekulu nebo částici zaujímající svůj průměrný tvar. |
|
3.1.2 |
překryvová koncentrace |
doporučený symbol: c*
Koncentrační oblast, v které je součet objemů domén zaujímaných molekulami nebo částicemi rozpuštěné látky přibližně roven celkovému objemu roztoku.
Poznámka
Význam termínu “doména” je vysvětlen v poznámce k 3.1.1. |
|
3.1.3 |
interakce mezi polymerem a rozpouštědlem, interakce polymer - rozpouštědlo |
Souhrn vlivů všech intermolekulárních interakcí mezi molekulami polymeru a rozpouštědla v roztoku, které se projevují v Gibbsově a Helmholtzově energii míšení. |
|
3.1.4 |
kvalita rozpouštědla, termodynamická kvalita rozpouštědla |
Kvalitativní charakterizace interakce polymer - rozpouštědlo (viz 3. l.3). Roztok polymeru v “lepším” rozpouštědle je charakterizován vyšší hodnotou druhého viriálního koeficientu (viz 3.1.7) než roztok téhož polymeru v “horším” rozpouštědle. |
|
3.1.5 |
stav theta |
Stav roztoku polymeru, ve kterém je druhý viriální koeficient (viz 3.1.7) roven nule.
Poznámky
1. V některých ohledech se roztok ve stavu theta podobá ideálnímu roztoku a tento stav můžeme označit za pseudoideální stav. Roztok ve stavu theta však nelze ztotožňovat s ideálním roztokem.
2. V literatuře se termín “stav theta” píše také jako “stav Q
”.
3. V tomto případě se rozpouštědlo často označuje jako “rozpouštědlo theta”.
4. Předpokládá se, že molární hmotnost polymeru je vysoká. |
|
3.1.6 |
teplota theta |
Teplota, při které je roztok ve stavu theta (viz 3.1.5).
Poznámka
V literatuře se termín “teplota theta” píše také jako "teplota Q
". |
|
3.1.7 |
viriální koeficienty, viriální koeficienty chemického potenciálu |
doporučený symbol: Ai, kde i =1, 2 atd.
Koeficienty rozvoje chemického potenciálu rozpouštědla, m
s, v mocninách hmotnostní koncentrace rozpuštěné látky, c, tj. rozvoje
m
s - m
s0 = - p
Vs = -RTVs(A1c+A2c2+A3c3 +...),
kde m
s0 je chemický potenciál rozpouštědla ve standardním stavu při teplotě systému a atmosférickém tlaku, p
je osmotický tlak a Vs je parciální molární objem rozpouštědla. V rozpouštědlech obsahujících více než jednu složku platí tato definice pro kteroukoli ze složek. První viriální koeficient je převrácená hodnota početně průměrné molární hmotnosti (viz 2.6), tj. 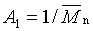 . Druhý a vyšší viriální koeficient A2, A3, ..., popisují interakce polymer - rozpouštědlo (viz 3.1.3) a polymer - polymer. . Druhý a vyšší viriální koeficient A2, A3, ..., popisují interakce polymer - rozpouštědlo (viz 3.1.3) a polymer - polymer.
Poznámka
Do viriálních koeficientů je někdy zahrnován i faktor RT. |
|
3.1.8 |
vyloučený objem segmentu |
Objem, z kterého segment makromolekuly v roztoku efektivně vylučuje všechny ostatní segmenty bez ohledu na to, zda náleží k téže makromolekule nebo k jiným makromolekulám.
Poznámka
Vyloučený objem segmentu závisí na Gibbsově a Helmholtzově energii míšení rozpouštědla a polymeru, tj. na termodynamické kvalitě rozpouštědla (viz 3.1.4), a není míro u geometrického objemu tohoto segmentu. |
|
3.1.9 |
vyloučený objem makromolekuly |
Objem, z kterého makromolekula ve zředěném roztoku efektivně vylučuje všechny ostatní makromolekuly.
Poznámka
Vyloučený objem makromolekuly závisí na Gibbsově a Helmholtzově energii míšení rozpouštědla a polymeru, tj. na termodynamické kvalitě rozpouštědla (viz 3.1.4), a není mírou geometrického objemu této makromolekuly. |
|
3.1.10 |
expanzní faktor |
doporučené symboly: a
r, a
s, a
h
Poměr rozměrové charakteristiky makromolekuly v daném rozpouštědle při dané teplotě k téže rozměrové charakteristice ve stavu theta (viz 3.1.5) při téže teplotě. Nejčastěji používané expanzní faktory jsou: expanzní faktor střední kvadratické vzdálenosti konců (viz 1.12) a
r =(á
r2ñ
á
r2ñ
0)1/2; expanzní faktor gyračního poloměru (viz 1.9) a
s=(á
s2ñ
á
s2ñ
0)1/2; viskozitní expanzní faktor a
h
=([h
]/[h
]q
)1/3, kde [h
] a [h
]q
jsou vnitřní viskozita (viz 3.2.21) v daném rozpoustědle a ve stavu theta při téže teplotě.
Poznámka
Expanzní faktory definované pomocí různých rozměrových charakteristik si nejsou přesně rovny a při měnící se relativní molekulové hmotnosti nemusí být jejich pomě r konstantní. |
|
3.1.11 |
Floryho-Hugginsova teorie |
Termodynamická teorie roztoků polymerů poprvé formulovaná nezávisle Florym a Hugginsem. Termodynamické veličiny roztoku jsou zde odvozeny z jednoduchého pojetí kombinatorické entropie míšení a parametru reduk ované Gibbsovy energie, parametru c
(viz 3.1.12). |
|
3.1.12 |
parametr c
|
doporučený symbol: c
Číselný parametr použitý ve Floryho-Hugginsově teorii (viz 3.1.11), který zahrnuje hlavně příspěvky nekombinatorické entropie míšení a entalpie míšení. |
|
3.1.13 |
preferenční sorpce, selektivní sorpce |
Rovnovážný jev uplatňující se v roztocích polymerů ve vícesložkových rozpoustědlech a v polymerních sítích (viz 1.26) nabotnalých vícesložkovými rozpouštědly. Spočívá v rozdílu mezi složením rozpouštědla v oblasti obsahující polymer a složením čistého rozpouštědla, které je v termodynamické rovnováze s touto oblastí. |
|
3.1.14 |
selektivní rozpouštědlo |
Prostředí, které je rozpouštědlem alespoň pro jednu složku směsi polymerů nebo alespoň pro jeden blok blokového nebo roubovaného polymeru, ale není rozpouštědlem pro ostatní složky nebo bloky. |
|
3.1.15 |
kosolvence |
Rozpouštění polymeru v rozpouštědle obsahujícím více složek, z nichž žádná není sama o sobě pro tento polymer rozpouštědlem. |
|
3.1.16 |
rozpustnostní parametr
(polymeru) |
doporučený symbol: d
Charakteristika polymeru používaná k předpovědi jeho rozpustnosti v daném rozpouštědle.
Poznámky:
1. U nízkomolekulárních látek se hodnota rozpustnostního parametru často odhaduje z výparné entalpie; u polymeru se za ni obvykle považuje hodnota rozpustnostního parametru rozpouštědla, jež s daným polymerem poskytne roztok o největší vnitřní viskozitě (viz 3.2.21) nebo vede k největšímu nabotnání sítě (viz 1.26).
2. Rozpustnostní parametr se obvykle vyjadřuje v jednotkách (cal/cm3)1/2 nebo lepe v (J/cm3)1/2. Jednotky musí byt vždy uvedeny; 1 (cal/cm3)1/2 = 2,05 (J/cm3)1/2. |
|
3.1.17 |
izopyknický |
Přívlastek označující složky vícesložkového systému, které mají stejný parciální specifický objem. |
|
3.2.1 |
frikční koeficient, koeficient tření |
doporučený symbol: f
Tenzor, který koreluje frikční sílu F, působící proti pohybu částice ve viskózní tekutině, a relativní rychlost u této částice vůči tekutině.
Poznámka
V případě izolované kulové částice ve viskózní izotropní kapalině je f konstanta a F = fu. |
|
3.2.2 |
hydrodynamicky ekvivalentní koule |
Hypotetická koule neprostupná pro okolní prostředí a vykazující v hydrodynamickém poli stejný frikční efekt jako skutečná molekula polymeru.
Poznámka
Velikost hydrodynamicky ekvivalentní koule se může lišit pro různé druhy pohybu makromolekuly, např. pro difúzi a pro viskózní tok. |
|
3.2.3 |
hydrodynamický objem |
Objem hydrodynamicky ekvivalentní koule (viz 3.2.2). |
|
3.2.4 |
model řetězce kuliček s tuhými spoji |
Model simulující hydrodynamické vlastnosti řetězovité makromolekuly složený z řady kuliček, z nichž každá klade toku okolního prostředí hydrodynamický odpor a je s nejbližší kuličkou spojena tuhou tyčinkou, která hydrodynamický odpor neklade. Vzájemná orientace tyčinek je nahodilá. |
|
3.2.5 |
model řetězce kuliček s pružnými spoji |
Model simulující hydrodynamické vlastnosti řetězovité makromolekuly složený z řady kuliček, z nichž každá klade toku okolního prostředí hydrodynamický odpor a je s nejbližší kuličkou spojena pružinou, která nepřispívá k frikční interakci, ale je nositelem elastických a deformačních vlastností řetězce. Vzájemná orientace pružin je nahodilá. |
|
3.2.6 |
volně průtočný |
Přívlastek označující řetězovitou makromolekulu, jejíž segmenty vyvolávají při pohybu prostředím tak malé frikční účinky, že hydrodynamické pole v okolí daného segmentu není přítomností ostatních segmentů ovlivněno. Rozpouštědlo tak může prakticky nerušeně protékat doménou, kterou zaujímá volně průtočná makromolekula. |
|
3.2.7 |
neprůtočný |
Přívlastek označující řetězovitou makromolekulu, která se v hydrodynamickém poli chová, jako by rozpouštědlo v doméně makromolekuly bylo vzhledem k makromolekule prakticky znehybněno. |
|
3.2.8 |
částečně průtočný |
Přívlastek označující řetězovitou makromolekulu, která se v hydrodynamickém poli chová, jako by rozpouštědlo v doméně makromolekuly bylo vzhledem k makromolekule znehybněno tím více, čím dále postupujeme od povrchu domény do jejího nitra.
Poznámka
Volně průtočná (viz 3.2.6.) makromolekula a neprůtočná (viz 3.2.7) makromolekula jsou dvě krajní meze pojmu částečně průtočné makromolekuly. |
|
3.2.9 |
dvojlom za toku |
Dvojlom vyvolaný tokem v kapalinách, roztocích a disperzích opticky anizotropních, anizometrických nebo deformovatelných molekul či částic a způsobený nenahodilou orientací molekul nebo částic. |
|
3.2.10 |
rotační difúze |
Děj, kterým se udržuje nebo obnovuje rovnovážná statistická distribuce celkové orientace molekul nebo částic.
Poznámka
Rotační difúze je obdobou translační difúze, kterou se udržuje nebo obnovuje rovnovážná statistická distribuce polohy částic v prostoru. |
|
3.2.11 |
sedimentační koeficient |
doporučený symbol: s
Parametr charakterizující pohyb částice v odstředivém poli a definovaný jako rychlost u pohybu způsobeného jednotkovým odstředivým zrychlením. Platí tedy s =
u/(r.w
2), kde u je rychlost pohybu, w
je úhlová rychlost a r je vzdálenost od středu otáčení.
Poznámka
Užitečnou jednotkou je 10 -13 sekundy; označuje se “svedberg”, který však není jednotkou soustavy SI. |
|
3.2.12 |
sedimentační rovnováha |
Rovnováha ustavená v odstředivém poli, kdy intenzita toku všech složek kteroukoli rovinou kolmou ke směru odstředivé síly je nulová. |
|
3.2.13 |
metoda sedimentační rovnováhy |
Metoda, kterou se za sedimentační rovnováhy (viz 3.2.12) stanovuje rozložení koncentrace rozpuštěné látky nebo disperzní složky ve zředěném roztoku nebo disperzi podél cely odstředivky a z výsledků se vyhodnocují molární hmotnosti (viz 1.2) nebo jejich di stribuce, anebo obojí. |
|
3.2.14 |
metoda sedimentační rychlosti |
Metoda, kterou se měří rychlost pohybu jedné nebo více rozpuštěných látek nebo disperzních částic a výsledek se vyjádří jako sedimentační koeficient (viz 3.2.11). |
|
3.2.15 |
Archibaldova metoda |
Sedimentační metoda založená na skutečnosti, že v menisku a na dně cely odstředivky nikdy nenastává tok rozpuštěné látky rovinou kolmou k radiálnímu směru a že tam vždy platí rovnice charakterizující sedimentační rovnováhu (viz 3.2.12), i když systém jako celek může být od rovnováhy vzdálen.
Poznámka
Pro Archibaldovu metodu se nedoporučuje používat termín "metoda přiblížení k sedimentační rovnováze", protože jeho význam je obecnějsí. |
|
3.2.16 |
rovnovážná sedimentace v gradientu hustoty |
Technika rovnovážné sedimentace (viz 3.2.13) pracující s vícesložkovým rozpouštědlem vytvářejícím v odstředivém poli gradient hustoty. |
|
3.2.17 |
relativní viskozita, viskozitní poměr |
doporučený symbol: h
r
Poměr viskozity roztoku h
k viskozitě rozpouštědla h
s, tj. h
r =h
/h
s. |
|
3.2.18 |
inkrement (relativní) viskozity |
doporučený symbol: h
i
Poměr rozdílu viskozity roztoku a viskozity rozpouštědla k viskozitě rozpoustědla, tj. h
i = (h
-h
s)/h
s. Význam symbolů viz 3.2.17.
Poznámka
Používání termínu “specifická viskozita” pro tuto veličinu se nedoporučuje, protože inkrement relativní viskozity nemá vlastnosti specifické veličiny. |
|
3.2.19 |
redukovaná viskozita, viskozitní číslo |
Poměr inkrementu relativní viskozity (viz 3.2.18) k hmotnostní koncentraci c polymeru, tj. h
i/c.
Poznámky
1. Jednotky musí být udány; doporučuje se cm 3/g.
2. Tato veličina a veličiny definované v 3.2.20 a 3.2.21 nejsou ani viskozity ani prostá čísla. Na tyto termíny je nutno pohlížet jako na tradiční názvy. Jejich náhrada konzistentními termíny by způsobila v literatuře o polymerech nežádoucí zmatek. |
|
3.2.20 |
inherentní viskozita, logaritmické viskozítní číslo |
doporučené symboly: h
inh, h
ln
Poměr přirozeného logaritmu relativní viskozity (viz 3.2.17) k hmotnostní koncentraci polymeru c, tj.
h
inh º
h
ln =(ln h
r)/c
Poznámka
Viz poznámky u 3.2.19. |
|
3.2.21 |
vnitřní viskozita, limitní viskozitní číslo |
doporučený symbol: [h
]
Limitní hodnota redukované viskozity (viz 3.2.19) nebo inherentní viskozity (viz 3.2.20) při nekonečném zředění polymeru, tj.
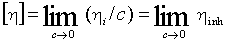
Poznámky
1. Tento termín je v literatuře znám jako Staudingerův index.
2. Viz poznámky u 3.2.19. |
|
3.2.22 |
Hugginsova rovnice |
Rovnice popisující závislost redukované viskozity (viz 3.2.19), h
i/c, na hmotnostní koncentraci polymeru c; pro zředěné roztoky (viz 3.1.1) má rovnice tvar
h
i/c = [h
] + kH[h
]2c
kde kH je Hugginsův koeficient (viz 3.2.23) a [h
] je vnitřní viskozita (viz 3.2.21). |
|
3.2.23 |
Hugginsův koeficient |
doporučený symbol: kH
Parametr v Hugginsově rovnici (viz 3.2.22). |
|
3.2.24 |
viskozitní funkce |
doporučený symbo l: F
Koeficient ve vztahu mezi vnitřní viskozitou (viz 3.2.21), gyračním poloměrem (viz 1.9) a molární hmotností (viz 1.2) řetězovité makromolekuly, podle rovnice
[h
] = F
63/2(s2)3/2/M
Poznámka Viskozitní funkce je často označována jako Floryho konstanta. |
|
3.2.25 |
Markova-Houwinkova rovnice |
Rovnice popisující závislost vnitřní viskozity (viz 3.2.21) polymeru na jeho relativní molekulové hmotnosti (viz 1.1), ve tvaru
[h
] = KMar
kde K a a jsou konstanty, jejichž hodnoty závisí na povaze polymeru a rozpouštědla a na teplotě; Mr je obvykle jeden z průměrů relativní molekulové hmotnosti (viz 2.5).
Poznámky
1. V této rovnici se doporučuje používat relativní molekulovou hmotnost spíše než molární hmotnost (která má rozměr hmotnosti dělené látkovým množstvím), protože v důsledku toho, že exponent a není celé číslo a nabývá různých hodnot, konstanta K má nepohodlný a proměnlivý rozměr.
2. Příspěvek Kuhna a Sakurady byl též významný a jejich jména bývají někdy zahrnuta do názvu rovnice, např. Kuhnova-Markova-Houwinkova-Sakuradova rovnice. |
|
Termín |
|
Definice |
|
3.3.1 |
malá částice |
Částice mnohem menší než vlnová délka záření v prostředí. V praxi, všechny rozměry částice považované za malou musí být menší než přibližně jedna dvacetina použité vlnové délk y. |
|
3.3.2 |
velká částice |
Částice s rozměry srovnatelnými s vlnovou délkou záření v prostředí nebo většími. V praxi je třeba považovat částici za velkou, překračuje-li její největší rozměr přibližně jednu dvacetinu použité vlnové délky. |
|
3.3.3 |
rozptylový úhel, úhel pozorování |
doporučený symbol: q
Úhel mezi směrem šíření primárního paprsku a přímkou spojující rozptylující bod s detektorem. |
|
3.3.4 |
rozptylový vektor |
Vektorový rozdíl vektorů šíření vlny dopadajícího a rozptýleného paprsku, obou o délce 2p
/l
, kde l
je vlnová délka rozptýleného záření v prostředí. |
|
3.3.5 |
délka rozptylového vektoru |
doporučený symbol: q
Délka rozptylového vektoru (viz 3.3.4) je q = (4p
/l
).sin (q
/2), kde l
je vlnová délka rozptýleného záření v prostředí a q
je rozptylový úhel (viz 3.3.3). |
|
3.3.6 |
inkrement indexu lomu |
doporučený symbol: d
n/d
C
Změna indexu lomu roztoku, n, s koncentrací rozpuštěné látky, C.
Poznámka
Koncentrace rozpuštěné látky se nejčastěji udává jako hmotnostní koncentrace, molalita nebo objemový zlomek. Je-li vyjádřena jako hmotnostní koncentrace nebo molalita, odpovídající inkrementy indexu lomu se označují jako specifické nebo molální inkrementy indexu lomu. |
|
3.3.7 |
Rayleighův poměr |
doporučen é symboly: R(q
), Rq
Veličina používaná k charakterizaci intenzity rozptylu při rozptylovém úhlu q
(viz 3.3.3), definovaná jako R(q
) = iq
r2/(I.f.V), kde I je intenzita dopadajícího záření, iq
je celková intenzita rozptýleného záření pozorovaná pod úhlem q
a ve vzdálenosti r od rozptylujícího bodu a V je rozptylující objem. Faktor f bere v úvahu vliv polarizačních jevů. Závisí na druhu použitého záření:
1. při rozptylu světla je podle polarizace dopadajícího paprsku f = 1 pro světlo polarizované vertikálně, f = cos2q
pro světlo polarizované horizontálně, f = (1+cos2q
)/2 pro nepolarizované světlo;
2. při maloúhlovém rozptylu neutronů f = 1;
3. při maloúhlovém rozptylu paprsků X je f = 1 pro q
menší než asi 5°.
Poznámky
1. Rozměr R(q
) je (délka)-1 a běžně používaná jednotka je cm-1.
2. V maloúhlovém rozptylu neutronů se místo Rayleighova poměru často používá termín rozptylový průřez; obě veličiny jsou totožné. |
|
3.3.8 |
dodatkový Rayleighův poměr |
Rozdíl mezi Rayleighovým poměrem (viz 3.3.7) zředěného roztoku a čistého rozpoustědla.
Poznámka
Není-li intenzita rozptylu převedena na Rayleighův poměr, nazývá se rozdíl mezi intenzitou rozptylu zředěného roztoku a čistého rozpouštědla “dodatkový rozptyl”. |
|
3.3.9 |
turbidita |
doporučený symbol: t
Zdánlivá absorbance dopadajícího záření způsobená rozptylem.
Poznámka
U malých částic (viz 3.3.1) je mezi turbiditou a Rayleighovým poměrem (viz 3.3.7) přímá úměrnost. |
|
3.3.10 |
rozptylová funkce částic, rozptylový faktor částic |
doporučené symboly: P(q
), Pq
Poměr intenzity záření rozptýleného v úhlu pozorování q
(viz 3.3.3) k intenzitě záření rozptýlené v nulovém úhlu, tj. P(q
) = R(q
)/R(0). |
|
3.3.11 |
Zimmův graf |
Grafické znázornění dat pro rozptyl velkými částicemi (viz 3.3.2) podle rovnice
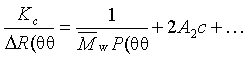
užívané pro současné vyhodnocení hmotnostně průměrné molární hmotnosti 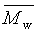 (viz 2.7), druhého viriálního koeficientu chemického potenciálu A2 (viz 3.1.7) a (obvykle) z-průměru gyračního poloměru (viz 2.7), druhého viriálního koeficientu chemického potenciálu A2 (viz 3.1.7) a (obvykle) z-průměru gyračního poloměru 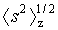 (viz 1.9); c je hmotnostní koncentrace rozpuštěné látky, D
R(q
) dodatkový Rayleighův poměr (viz 3.3.8) a P(q
) rozptylová funkce částic (viz 3.3.10), která (obvykle) obsahuje z-průměr gyračního poloměru. K závisí na rozpuštěné látce, teplotě a druhu použitého záření. (viz 1.9); c je hmotnostní koncentrace rozpuštěné látky, D
R(q
) dodatkový Rayleighův poměr (viz 3.3.8) a P(q
) rozptylová funkce částic (viz 3.3.10), která (obvykle) obsahuje z-průměr gyračního poloměru. K závisí na rozpuštěné látce, teplotě a druhu použitého záření.
Poznámka
Často se užívá modifikací Zimmova grafu; nejobvyklejší z nich používá dodatkového rozptylu místo dodatkového Rayleighova poměru (viz 3.3.8). |
|
3.3.12 |
Guinierův graf |
Grafické znázornění dat pro rozptyl velkými částicemi (viz 3.3.2), získaných při různých úhlech, avšak při téže koncentraci, se strojené vynesením log D
R (q
) nebo log P(q
) proti sin2(q
/2) nebo q2 a (obvykle) užívané pro vyhodnocení gyračního poloměru (viz 1.9). D
R(q
), je dodatkový Rayleighův poměr (viz 3.3.8), P(q
) rozptylová funkce částic (viz 3.3.10), q
rozptylový úhel (viz 3.3.3) a q délka rozptylového vektoru (viz 3.3.5). |
|
3.3.13 |
Kratkyho graf |
Grafické znázornění dat pro rozptyl velkými částicemi (viz 3.3.2), získaných při různých úhlech, avšak při téže koncentraci, sestrojené vynesením sin 2 (q
/2).D
R(q
) proti sin(q
/2) nebo q2 D
R(q
) proti q, a užívané pro určení tvaru molekul. Význam symbolů viz 3.3.12. |
|
3.3.14 |
dissymetrie rozptylu |
doporučený symbol: z(q
1,q
2)
Podíl Rayleighových poměrů (viz 3.3.7) stanovených při dvou různých úhlech pozorování (viz 3.3.3), tj. z(q
1,q
2) = R(q
1,q
2) = R(q
1)/R(q
2), q
1<
q
2.
Poznámka
Úhly musí být udány; při použití metody rozptylu světla se obvykle volí q
2 =180°-q
1, nejčastěji q
1 = 45° a q
2 =135°. |
|
3.3.15 |
depolarizace rozptýleného světla |
Jev způsobený především anizotropií polarizovatelnosti rozptylujícího prostředí a vyplývající ze skutečnosti, že elektrické vektory dopadajícího a rozptýleného paprsku nejsou koplanární a že proto světlo rozptýlené z vertikálně (horizontálně) polarizovaného dopadajícího paprsku má horizontální (vertikální) složku. |
|
3.3.16 |
turbidimetrická titrace |
Proces, při němž se postupně přidává srážedlo k velmi zředěnému roztoku polymeru a měří se intenzita světla rozptýleného jemně dispergovanými částicemi fáze bohaté polymerem (viz 3.4.3), nebo turbidita (viz 3.3.9) jimi způsobená, jako funkce množství přidaného srážedla |
|
3.3.17 |
izorefraktivní |
Přívlastek charakterizující složky vícesložkového systému, které mají navzájem nulové ink rementy indexu lomu (viz 3.3.6). |
|
3.3.18 |
Mieův rozptyl |
Rozptyl světla částicemi rozměrů větsích než přibližně polovina vlnové délky dopadajíci'ho světla
Poznámka
Pro homogenní koule je tento jev rigorózně popsán teorií, kterou vypracoval Mie. |
| |
|
|
|
3.4.1 |
frakcionace |
Proces, kterým se od sebe oddělují druhy makromolekul lišící se nějakou charakteristikou (chemickým složením, relativní molekulovou hmotností (viz 1.1), větvením, stereoregularitou atd.). |
|
3.4.2 |
fáze chudá polymerem,
zředěná fáze |
Ta fáze dvoufázového rovnovážného systému skládajícího se z polymeru a nízkomolekulární látky, v níž je koncentrace polymeru nižší.
Poznámka
Používání názvu “solová fáze” se nedoporučuje |
|
3.4.3 |
fáze bohatá polymerem, koncentrovaná fáze |
Ta fáze dvoufázového rovnovážného systému skládajícího se z polymeru a nízkomolekulární látky, v níž je koncentrace polymeru vyšší.
Používání názvu “gelová fáze” se nedoporučuje. |
|
3.4.4 |
srážecí frakcionace |
Proces, jímž se polymer, obsahující makromolekuly, které se liší nějakou charakteristikou ovlivňující jejich rozpustnost, vylučuje z roztoku ve frakcích postupným snižováním rozpouštěcí schopnosti rozpouštědla; to vede k vzniku dvoufázového systému, v němž se méně rozpustné složky koncentrují ve fázi bohaté polymerem (viz 3.4.3). |
|
3.4.5 |
extrakční frakcionace |
Proces, jímž se polymer, obsahující makromolekuly, které se liší nějakou charakteristikou ovlivňující jejich rozpustnost, odděluje z fáze bohaté polymerem (viz 3.4.3) ve frakcích postupným zvyšováním rozpouštěcí schopnosti rozpouštědla; to opakovaně vede k vzniku dvoufázového systému, v němž se rozpustnější složky koncentrují ve fázi chudé polymerem (viz 3.4.2). |
|
3.4.6 |
rozměrově vylučovací chromatografie |
doporučená zkratka: SEC
Separační technika, při níž dělení probíhá hlavně podle hydrodynamického objemu (viz 3.2.3) molekul nebo částic, a to v porézním neadsorbujícím materiálu, jehož póry mají přibližně stejnou velikost jako efektivní rozmě ry separovaných molekul v roztoku. |
| |
gelová permeační chromatografie |
doporučená zkratka: GPC
Název “gelová permeační chromatografie” by se měl užívat pouze, pokud porézním neadsorbujícím materiálem je gel. Názvu “rozměrové vylučovací chromatografie” se dává přednost. |
|
3.4.7 |
vylučovací mez molární hmotnosti, vylučovací mez relativní molekulové hmotnosti |
Největší hodnota molární hmotnosti (viz 1.2) nebo relativní molekulové hmotnosti (viz 1.1) molekul nebo částic, které mohou pronikat do pórů porézního neadsorbujícího materiálu používaného v rozměrově vylučovací chromatografii (viz 3.4.6) v určitém systému polymer - rozpouštědlo.
Poznámka
Pro částice s molární hmotností nebo relativní molekulovou hmotností větší než vylučovací mez dělící účinek rozměrově vylučovací chromatografie mizí. |
|
3.4.8 |
eluční objem |
Objem rozpouštědla proteklého ložem při rozměrově vylučovací chromatografii (viz 3.4.6) od nástřiku vzorku do doby, kdy je zaznamenán určitý signál detektoru. |
|
3.4.9 |
retenční objem
|
Eluční objem (viz 3.4.8) v koncentračním maximu elučního píku. |
|
3.4.10 |
univerzální kalibrace |
Kalibrace zařízení po rozměrově vylučovací chromatografii (viz 3.4.6) založená na poznatku, že retenční objem (viz 3.4.9) molekul nebo částic je jednoznačnou funkcí vhodného parametru charakterizujícího velikost této molekuly nebo částice bez ohledu na chemickou povahu a strukturu.
Poznámka
Jako parametr charakterizující velikost se často používá součin vnitřní viskozity (viz 3.2.21) a molární hmotnosti (viz 1.2), [h
]M. |
|
3.4.11 |
funkce rozmytí |
Normovaný signál na výstupu ze zařízení pro rozměrově vylučovací chromatografii (viz 3.4.6), způsobený okamžitým nástřikem uniformního vzorku, jako funkce elučního objemu (viz 3.4.8). |
|
3.4.12 |
počet pater |
doporučený symbol: N
Charakteristika účinnosti zařízení pro rozměrově vylučovací chromatografii (viz 3.4.6) vyjádřená rozšířením pásu a definovaná jako N = (VR/σV)2, kde VR je retenční objem (viz 3.4.9) jednotlivě nízkomolekulární sloučeniny a σV je poloviční šířka elučního píku při 60,7% jeho výšky. |
|
3.4.13 |
výška patra |
doporučený symbol: H
Délka lože pro rozměrově vylučovací chromatografii (viz 3.4.6) odpovídající jednomu patru, tj. délka lože L dělená počtem jeho pater N (viz 3.4.12), tedy H = LlN. |
4. Abecední seznam termínů
|
Český termín |
Anglický termín |
Symbol |
Číslo definic |
|
Archibaldova metoda |
Archibald's method |
|
3.2.15 |
|
částečně průtočný |
partially draining |
|
3.2.8 |
|
červovitý řetězec |
worm-like chain |
|
1.21 |
|
délka rozptylového vektoru |
length of the scattering vector |
q |
3.3.5 |
|
depolarizace rozptýleného světla |
depolarization of scattered light |
|
3.3.15 |
|
diferenciální distribuční funkce |
differential distribution function |
|
2.13 |
|
diskrétní distribuční funkce |
differential distribution function |
|
2.13 |
|
dissymetrie rozptylu |
dissymetry of scattering |
z(q
1q
2) |
3.3.14 |
|
distribuční funkce |
distribution function |
|
2.13 |
|
dlouhá větev |
long-chain branch |
|
1.24 |
|
dodatkový Rayleighův poměr |
excess Rayleigh ratio |
|
3.3.8 |
|
dodatkový rozptyl |
excess scattering |
|
3.3.8 |
|
druhý viriální koeficient |
second virial coefficient |
A2 |
3.1.7 |
|
dvojlom za toku |
flow birefringence (streaming birefringence) |
|
3.2.9 |
|
ekvivalentní koule |
equivalent sphere |
|
1.4, 3.2.2 |
|
ekvivalentní řetězec |
equivalent chain |
|
1.17 |
|
eluční objem |
elution volume |
|
3.4.8 |
|
expanzní faktor |
expansion factor |
a
r, a
s, a
q
|
3.1.10 |
|
extrakční frakcionace |
extraction fractionation |
|
3.4.5 |
|
fáze bohatá polymerem |
polymer-rich phase |
|
3.4.3 |
|
fáze chudá polymerem |
polymer-poor phase |
|
3.4.2 |
|
Floryho distribuce |
Flory distribution |
|
2.17 |
|
Floryho-Hugginsova teorie |
Flory-Huggins theory |
|
3.1.11 |
|
Floryho konstanta |
Flory constant |
F
|
3.2.24 |
|
frakcionace |
fractionation |
|
3.4.1 |
|
frikční koeficient |
frictional coefficient |
f |
3.2.1 |
|
funkce rozmytí |
spreading function |
|
3.4.11 |
|
gelová permeační chromatografie |
gel-permeation chromatography |
|
3.4.6 |
|
Guinierův graf |
Guinier plot |
|
3.3.12 |
|
gyrační poloměr |
radius of gyration |
s, á
s2ñ
1/2 |
1.9 |
|
heterogenita ve složení |
compositional heterogeneity |
|
2.1 |
|
hmotnostně průměrná molární hmotnost |
mass-average molar mass |
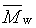
|
2.7 |
|
hmotnostně průměrná relativní molekulová hmotnost |
mass-average relative molecular mass / weight-average molecular weight |
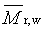
|
2.7 |
|
hmotnostní distribuční funkce |
mass distribution function |
|
2.15 |
|
hmotnostně průměrný polymerizační stupeň |
mass-average degree of polymerization |
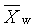
|
2.12 |
|
Hugginsova rovnice |
Huggins equation |
|
3.2.22 |
|
Hugginsův koeficient |
Huggins coefficient |
kH |
3.2.23 |
|
hydrodynamicky ekvivalentní koule |
hydrodynamically equivalent sphere |
|
3.2.2 |
|
hydrodynamický objem |
hydrodynamic volume |
|
3.2.3 |
|
charakteristický poměr |
characteristic ratio |
CN, C¥
|
1.13 |
|
index větvení |
branching index |
g |
1.25 |
|
inherentní viskozita |
inherent viscosity |
h
inh |
3.2.20 |
|
inkrement indexu lomu |
relative index increment |
d
n/d
C |
3.3.6 |
|
inkrement relativní viskozity |
relative viscosity increment |
h
i |
3.2.18 |
|
integrální distribuční funkce |
integral distribution function |
|
2.13 |
|
interakce dalekého dosahu |
long-range interaction |
|
1.6 |
|
interakce krátkého dosahu |
short-range interaction |
|
1.5 |
|
interakce mezi polymerem a rozpoustědlem |
polymer - solvent interaction |
|
3.1.3 |
|
intramolekulární interakce dalekého dosahu |
long-range intramolecular interaction |
|
1.6 |
|
intramolekulární interakce krátkého dosahu |
short-range intramolecular interaction |
|
1.5 |
|
izopyknický |
isopycnic |
|
3.1.17 |
|
izorefraktivní |
isorefractive |
|
3.3.17 |
|
koeficient tření |
frictional coefficient |
f |
3.2.1 |
|
koncentrovaná fáze |
concentrated phase |
|
3.4.3 |
|
konstituční heterogenita |
constitutional heterogeneity |
|
2.2 |
|
kopolymerní micela |
copolymer micelle |
|
1.28 |
|
korekce na polymolekularitu |
polymolecularity correction |
|
2.21 |
|
kosolvence |
co-solvency |
|
3.1.15 |
|
krátká větev |
short-chain branch |
|
1.23 |
|
Kratkyho graf |
Kratky plot |
|
3.3.13 |
|
Kuhnova-Markova-Houwinkova-Sakuradova rovnice |
Kuhn-Mark-Houwink-Sakurada equation |
|
3.2.25 |
|
kumulativní distribuční funkce |
cumulative distribution function |
|
2.13 |
|
kvalita rozpoustědla |
quality of solvent |
|
3.1.4 |
|
limitní viskozitní číslo |
limiting viscosity number |
[h
] |
3.2.21 |
|
logaritmická normální distribuce |
logarithmic normal dislribution |
|
2.20 |
|
logaritmické viskozitní číslo |
logarithmic viscosity number |
h
ln |
3.2.20 |
|
malá částice |
small particle |
|
3.3.1 |
|
Markova-Houwinkova rovnice |
Mark-Houwink equation |
|
3.2.25 |
|
metoda sedimentační rovnováhy |
equilibrium sedimentation method |
|
3.2.13 |
|
metoda sedimentační rychlosti |
sedimentation velocity method |
|
3.2.14 |
|
Mieův rozptyl |
Mie scattering |
|
3.3.18 |
|
mikrogel |
microgel |
|
1.27 |
|
model řetězce kuliček s tuhými spoji |
bead-rod model |
|
3.2.4 |
|
model řetězce kuliček s pružnými spoji |
bead-spring model |
|
3.2.5 |
|
molární inkrement indexu lomu |
molal refractive index increment |
|
3.3.6 |
|
molární hmotnost |
molar mass |
M |
1.2 |
|
monodisperzní polymer |
monodisperse polymer |
|
2.3 |
|
nahodilé klubko |
random coil |
|
1.15 |
|
nejpravděpodobnější distribuce |
most propable distribution |
|
2.17 |
|
neporušené rozměry |
unperturbed dimensions |
|
1.7 |
|
neprůtočný |
non-draining |
|
3.2.7 |
|
neuniformní polymer |
non-uniform polymer |
|
2.4 |
|
obrysová délka |
contour length |
|
1.14 |
|
odmocnina střední kvadratické vzdálenosti konců |
root-mean-square end-to-end distance |
á
r2ñ
1/2 |
1.12 |
|
parametr c
|
c
parameter |
c
|
3.1.12 |
|
perzistenční délka |
persistence length |
a |
1.22 |
|
počet pater |
plate number |
N |
3.4.12 |
|
početně průmerná molární hmotnost |
number-average molar mass |
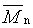
|
2.6 |
|
početně průměrná relativní molekulová hmotnost |
number-average relative molecular mass/number-average molecular weight |
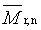
|
2.6 |
|
početně průměrný polymerizační stupeň |
number-average degree of polymerization |
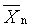
|
2.12 |
|
početní distribuční funkce |
number-distribution function |
|
2.14 |
|
Poissonova distribuce |
Poisson distribution |
|
2.18 |
|
polydisperzní polymer |
polydisperse polymer |
|
2.4 |
|
polymerizační stupeň |
degree of polymerization |
X |
1.3 |
|
Porodův a Kratkyho řetězec |
Porod-Kratky chain |
|
1.21 |
|
porušené rozměry |
perturbed dimensions |
|
1.8 |
|
pravděpodobnostně hustotní funkce |
probability density function |
|
2.13 |
|
preferenční sorpce |
preferental sorption |
|
3.1.13 |
|
překryvová koncentrace |
cross-over concentration |
c* |
3.12 |
|
průměr molární hmotnosti |
molecular-mass average/ molecular-weight average |
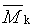
|
2.5 |
|
průměr relativní molekulové hmotnosti |
relative molecular-mass average |
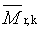
|
2.5 |
|
průměrný polymerizační stupeň |
average degree of polymerization |
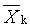
|
2.12 |
|
Rayleighův poměr |
Rayleigh ratio |
R(q
), Rq
|
3.3.7 |
|
redukovaná viskozita |
reduced viscosity |
|
3.2.19 |
|
relativní molekulová hmotnost |
relative molecular mass/ relative molecular weight |
Mr |
1.1 |
|
relativní viskozita |
relative viscosity |
h
r |
3.2.17 |
|
retenční objem |
retention volume |
|
3.4.9 |
|
rotační difúze |
rotational diffusion |
|
3.2.10 |
|
rovnovážná sedimentace v gradientu hustoty |
equilibrium sedimentation in a density gradient |
|
3.2.16 |
|
rozměrově vylučovací chromatografie |
size-exclusion chromatography |
|
3.4.6 |
|
rozpouštědlo theta |
theta solvent (Q
solvent) |
|
3.1.5 |
|
rozptylová funkce částic |
particle scattering function |
P(q
), Pq
|
3.3.10 |
|
rozptylový faktor částic |
particle scattering factor |
P(q
), Pq
|
3.3.10 |
|
rozptylový průřez |
seaffering cross-section |
|
3.3.7 |
|
rozptylový úhel |
scattering angle |
q
|
3.3.3 |
|
rozptylový vektor |
scattering vector |
|
3.3.4 |
|
rozpustnostní parametr |
solubility parameter |
d
|
3.1.16 |
|
řetězec typu nahodilé procházky |
random-walk chain |
|
1.16 |
|
sedimentační koeficient |
sedimentation coefficient |
s |
3.2.11 |
|
sedimentační rovnováha |
sedimentation equilibrium |
|
3.2.12 |
|
selektivní rozpoustědlo |
selective solvent |
|
3.1.14 |
|
selektivní sorpce |
selective sorption |
|
3.1.13 |
|
síť |
network |
|
1.26 |
|
Schulzova-Floryho distribuce |
Schulz-Flory distribution |
|
2.17 |
|
Schulzova-Zimmova distribuce |
Schulz-Zimm distribution |
|
2.16 |
|
specifický inkrement indexu lomu |
specific refractive index increment |
|
3.3.6 |
|
spojitá distribuční funkce |
continuous distribution function |
|
2.13 |
|
spojitě zakřivený řetězec |
continuously curved chain |
|
1.21 |
|
srážecí frakcionace |
precipitation fractionation |
|
3.4.4 |
|
statistické klubko |
statistical coil |
|
1.15 |
|
statistický segment |
statistical segment |
|
1.18 |
|
Staudingerův index |
Staudinger index |
[h
] |
3.2.21 |
|
stav theta |
theta state (Q
state) |
|
3.1.5 |
|
sterický faktor |
steric factor |
s
|
1.20 |
|
stupeň polymerizace |
degree of polymerization |
X |
1.3 |
|
teplota theta |
theta temperature (Q
temperature) |
|
3.1.6 |
|
telmodynamická kvalita rozpouštědla |
thermodynamic quality of solvent o |
|
3.1.4 |
|
tertnodynamicky ekvivalentní koule |
thermodynamically equivalent sphere |
|
1.4 |
|
Tungova distribuce |
Tung distribution |
|
2.19 |
|
turbidimetrická titrace |
turbidimetric titration |
|
3.3.16 |
|
turbidita |
turbidity |
t
|
3.3..9 |
|
úhel pozorování |
angle of observation |
q
|
3.3.3 |
|
uniformní polymer |
uniform polymer |
|
2.3 |
|
univerzální kalibrace |
universal calibration |
|
3.4.10 |
|
vektor spojnice konců |
end-to-end vector |
r |
1.10 |
|
velká čá stice |
large particle |
|
3.3.2 |
|
viriální koeficienty chemického potenciálu |
virial coefficients of the chemical potential |
A1, A2… |
3.1.7 |
|
viskozitní číslo |
viscosity number |
|
3.2.19 |
|
viskozitní funkce |
viscosity function |
F
|
3.2.24 |
|
viskozitní poměr |
viscosity ratio |
h
r |
3.2.17 |
|
viskozitně průměrná molární hmotnost |
viscosity-average molar mass |
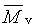
|
2.10 |
|
viskozitně průměrná relativní molekulová hmot nost |
viscosity-average relative molecular mass / viscosity-average molecular weight |
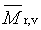
|
2.10 |
|
viskozitně průměrný polymerizační stupeň |
viscosity-average degree of polymerization |
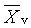
|
2.12 |
|
vnitřní viskozita |
intrinsic viscosity |
[h
] |
3.2.21 |
|
volně průtočný |
freely draining |
|
3.2.6 |
|
volně otáčivý řetězec |
freely rotating chain |
|
1.19 |
|
volně skloubený řetězec |
freely jointed chain |
|
1.16 |
|
vyloučený objem makromolekuly |
excluded volume of a macromolecule |
|
3.1.9 |
|
vyloučený objem segmentu |
excluded volume of a segment |
|
3.1.8 |
|
vylučovací mez molekulové hmotnosti |
molecular - weight exclusion limit |
|
3.4.7 |
|
vylučovací mez mol ární hmotnosti |
molar-mass exclusion limit |
|
3.4.7 |
|
výška patra |
plate height |
H |
3.4.13 |
|
vzdálenost konců |
end-to-end distance |
r |
1.11, 1.12 |
|
zdánlivá molámí hmotnost |
apparent molar mass |

|
2.11 |
|
zdánlivá relativní molekulová hmotnost |
apparent relative molecular mass |
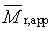
|
2.11 |
|
Zimmův graf |
Zimm plot |
|
3.3.11 |
|
z-průměrná molární hmotnost |
z-average molar mass |
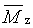
|
2.8 |
|
z-průměrná relativní molekulová hmotnost |
z-average relative molecular mass/ z-average molecular weight |
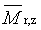
|
2.8 |
|
z-průmerný polymerizační stupeň |
z-average degree of polymerization |
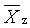
|
2.12 |
|
(z+1)-průměrná molární hmotnost |
(z+1)-average molar mass |
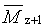
|
2.9 |
|
(z+1)-průměrná relativní molekulová hmotnost |
(z+1)-average relative molecular mass |
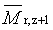
|
2.9 |
|
(z+1)-průměrný polymerizační stupeň |
(z+1)-average degree of polymerization |
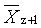
|
2.12 |
|
zředen á fáze |
dilute phase |
|
3.4.2 |
|
zředěný roztok |
dilute solution |
|
3.1.1 |
5. Literatura
1. Basic Definitions of Terms Relating to Polymers (1974), Pure Appl. Chem. 40, 477 (1974); Compendium of MacromolecularNomenclature, Blackwell Scientific Publications, Oxford 1991, str. 13-24. České znění Chem. Listy 79, 281 (1985).
2. Stereochemical Definitions and Notations Relating to Polymers (Recommendations 1980), Pure Appl. Chem. 53, 733 (1981); Compendium of Macromolecular Nomenclature, Blackwell Scientific Publications, Oxford 1991, str. 25-46.
3. Note on the Terminology for Molar Masses in Polymer Science, Makromol. Chem. 185, Appendix to No. l (1984); J. Polym. Sci., Polym. Lett. Ed. 22, S7 (1984).
![]()
![]()
![]()
![]()